https://leetcode.com/problems/unique-paths/description
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Q. 아래와 같이 주어진 m x n grid 에서 로봇이 좌상단에 있다. 우하단으로 도달하기 위한 모든 경로의 수를 찾아라.
이때 로봇은 우로 혹은 아래로 1칸만 이동 가능하다.
Solution.
특정 위치로 도달하는 경우의 수를 찾는 문제다. 도달하면서 과정사이의 어떤 값을 누적 하는것이 아니고,
목표위치로 로달하기만 하면 분기하는 과정에서 경로는 어찌됐는 유일하므로, 1가지가 추가가 되는 것이다.
DP의 특성상 특정 위치에서 일반화 해 보자.
우측 혹은 아래로 모두 갈 수 있는 아래 붉은 원 지점에서 도달하는 경우의 수는 2가지 된다.

하지만 아래 붉은 원 지점에서는 3가지가 된다.
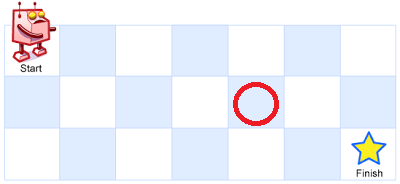
즉, 특정 grid에서의 갈수 있는 경우의 수의 합은
진행 과정에서의 grid 에서 갈수있는 수의 총합이라는 것을 알수 있다.
따라서 현재 로봇의 위치에서는, 우측방향 grid에서의 경우의 수(2) + 아래 grid에서의 경우의 수(1) 라는 것을 알 수 있고,
위 위치에서는 2+1 해서 3이 된다.
total count = f(x+1) + f(y+1)
다만 x나 y가 m, n의 한계에 부딪히면 한 방향으로만 진행 가능하다.
이를 코드를 작성해 본다.
int uniquePaths_dp(int x, int y, int m, int n)
{
if(x==m-1 && y==n-1)
return 1;
int nLeft = 0, nRight = 0;
if(x < m-1) nLeft = uniquePaths_dp(x+1, y, m, n);
if(y < n-1) nRight = uniquePaths_dp(x, y+1, m, n);
return nLeft + nRight;
}
public:
int uniquePaths(int m, int n)
{
return uniquePaths_dp(0, 0, m, n);
}
로직을 그대로 코드를 옮긴 것이다.
자주보는 에러를 본다.

최적화를 진행 해 본다.
int uniquePaths_dp(int x, int y, int m, int n, vector<int>& vCache)
{
if(x==m-1 && y==n-1)
return 1;
int idx = y*m + x;
if(vCache[idx] >= 0)
return vCache[idx];
int nLeft = 0, nRight = 0;
if(x < m-1) nLeft = uniquePaths_dp(x+1, y, m, n, vCache);
if(y < n-1) nRight = uniquePaths_dp(x, y+1, m, n, vCache);
vCache[idx] = nLeft + nRight;
return vCache[idx];
}
public:
int uniquePaths(int m, int n)
{
vector<int> vCache;
vCache.resize(m*n, -1);
return uniquePaths_dp(0, 0, m, n, vCache);
}
잘 통과 하였다.

'Leetcode > LeetCode75' 카테고리의 다른 글
| [DP-MultiDimensional][Medium] 72. Edit Distance (1) | 2024.01.28 |
|---|---|
| [DP-Multidimensional][Medium] 714. Best Time to Buy and Sell Stock with Transaction Fee. (1) | 2024.01.26 |
| [DP-1D][Medium] 790. Domino and Tromino Tiling (0) | 2024.01.19 |
| [DP-1D][Medium] 198. House Robber (0) | 2024.01.16 |
| [DP-1D][Easy] 746. Min Cost Climbing Stairs (0) | 2024.01.16 |