https://leetcode.com/problems/domino-and-tromino-tiling
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Q. 아래와 같은 두 종류의 shape이 존재할때, 2xn의 보드를 채운다면 몇가지 방법으로 가능할지 계산하라.
이때 결과가 너무 클 수 있으니, modulo는 10000000007 을 사용하라.
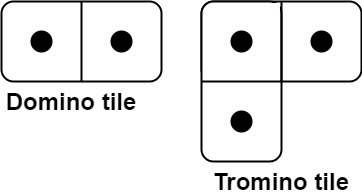
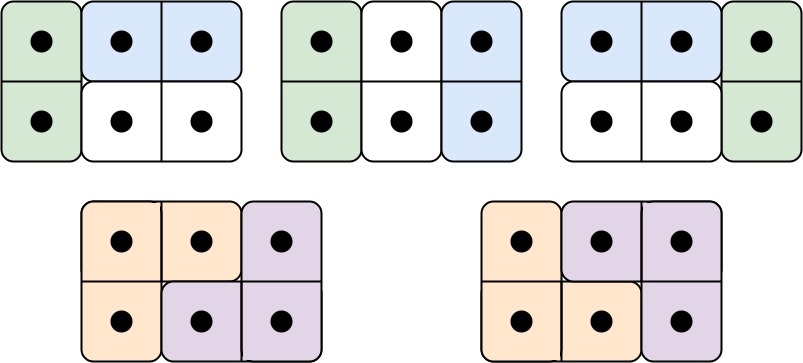
n=3 일 경우 예시
Solution.
직관으로 풀기는 어려운 문제다.
우선 타일 기반의 DP문제에 좀 익숙해야 할 것이다.
또한 이 타일들의 속성에서 공통점을 찾아 기본 로직, 즉 점화식을 만들어야 할 것인데, 이것도 직관으로는 쉽지 않다.
머릿속으로 여러번 우선 정리가 좀 필요해 보인다.
다소의 조사 후, 확장 시, 아래와 같은 속성이 있다는 것을 찾을 수 있었다.
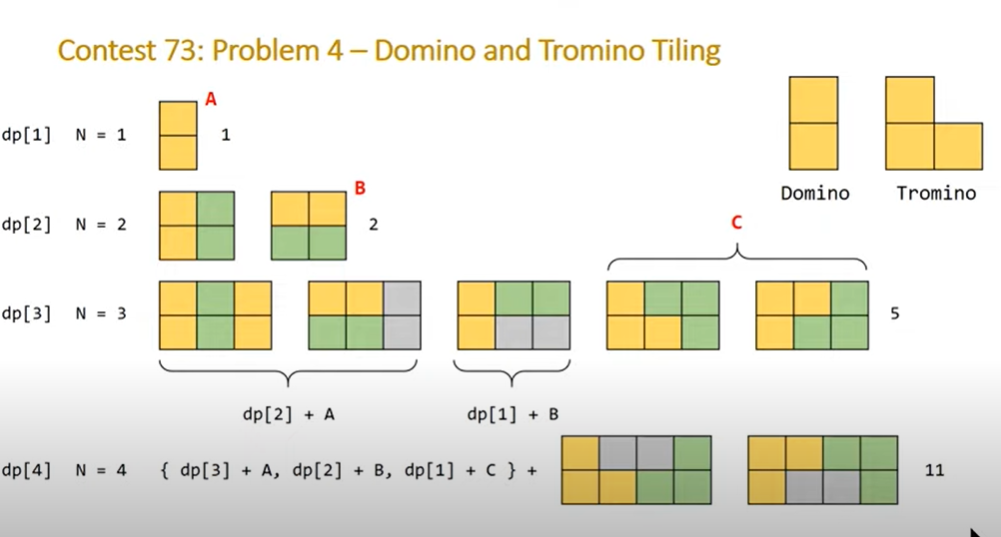
N = 1 인 경우, 세로로 세운 단 한가지만 가능하다.
N = 2 인 경우, 세로로 두줄, 가로로 두줄, 이렇게 두가지만 가능하다.
N = 3 인 경우, 한줄짜리를 활용하여 3개, tromino를 사용하여 두개가 가능함을 알았다.
N = 4 인 경우, 이런 식으로 확장된다.
(직접 연습장에 그려보면 조금 더 잘 보인다.)
즉, 보면,
N 위치에서
N-1 에 세로로 domino를 붙힌 꼴 하나 f(N-1)
N-2 에 domino를 가로로 둘 붙힌 꼴 하나 f(N-2)
N-3 에 2개의 tromino type을 붙이는 경우, 즉 두개 f(N-3) x 2,
(이 경우가 N==1 이 될때까지 계속 됨을 알 수 있다.)
그리고 N서 새로이 추가되는 tromino 기반의 2개의 추가 확장이 생긴다.
(note : 여기의 확장 일반화 로직을 찾는 것이, 직관으로 가능해 보이지 않는다. 더 일반화된 로직기반의 확장방법이 있는지 추후 조사가 필요.)
따라서 위를 근거로 점화식을 만들어 보면
f(n) = f(n-1) + f(n-2) + 2 x (f(n-3) + .... + f(1)) + 2
의 꼴이 된다.
이를 기반으로 코드를 만들어 본다.
int tiling_help(int idx)
{
if (idx == 0) return 1;
else if (idx == 1) return 2;
else if (idx == 2) return 5;
const long mod = 1000000007;
long sum = 0;
for (int q = idx - 3; q >= 0; --q)
{
sum += tiling_help(q);
sum %= mod;
}
return (tiling_help(idx - 1) + tiling_help(idx - 2) + sum * 2 + 2) % mod;
}
int numTilings(int n)
{
return tiling_help(n - 1);
}
캐싱없는 DP의 결과는 leetcode에서 자명하다.
캐싱을 넣어 다시 코드를 수정한다.
int tiling_help(vector<int>& vCache, int idx)
{
if (idx == 0) return 1;
else if (idx == 1) return 2;
else if (idx == 2) return 5;
if (vCache[idx] >= 0)
return vCache[idx];
const long mod = 1000000007;
long sum = 0;
for (int q = idx - 3; q >= 0; --q)
{
sum += tiling_help(vCache, q);
sum %= mod;
}
vCache[idx ] = (tiling_help(vCache, idx - 1) + tiling_help(vCache, idx - 2) + sum * 2 + 2) % mod;
return vCache[idx];
}
int numTilings(int n)
{
vector<int> vCache;
vCache.resize(n, -1);
return tiling_help(vCache, n - 1);
}
가까스로 cut 라인을 넘었다.

추가 조사 및 리포스팅 할 사안으로 일단 아래 목록을 남긴다.
1. DP의 추가 최적화 방안 / 재귀함수 회피법.
2. 10^9 + 7로 결과를 나누는 것은 int의 overflow를 피하기 위함이다. 이에 대한 세부 원리.
'Leetcode > LeetCode75' 카테고리의 다른 글
| [DP-Multidimensional][Medium] 714. Best Time to Buy and Sell Stock with Transaction Fee. (1) | 2024.01.26 |
|---|---|
| [DP-Multidimensional][Medium] 62. Unique Paths (1) | 2024.01.21 |
| [DP-1D][Medium] 198. House Robber (0) | 2024.01.16 |
| [DP-1D][Easy] 746. Min Cost Climbing Stairs (0) | 2024.01.16 |
| [DP-1D][Easy] 1137.N-th Tribonacci Number (1) | 2024.01.15 |