https://leetcode.com/problems/n-queens/description/
아래와 같은 N-Queens 를 만든다고 할때, n 이 주어지면 이에 가능한 N-Queens를 모두 찾아라.
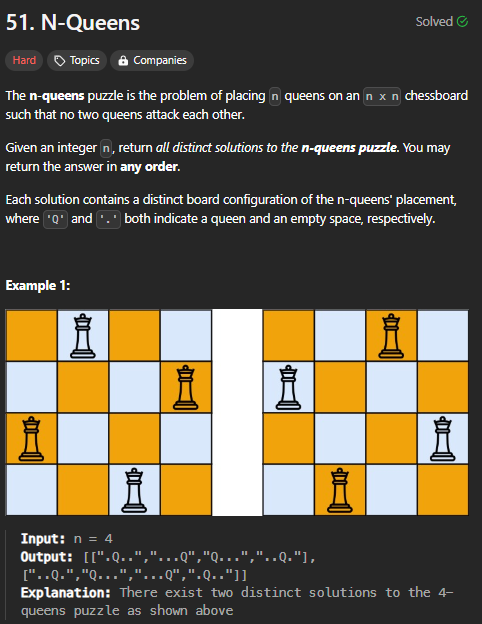
문제 자체는 쉽다.
매 칸당 Queen을 놓을 수 있다면, 놓거나 아니면 놓지 않는다.
코드
더보기
bool CanPlace(int idx, const vector<string>& vCur, int n)
{
int y = idx / n;
int x = idx % n;
// check H
for(int h = 0; h < n; ++h)
{
if(h!=x && vCur[y][h]=='Q')
return false;
}
// check V
for(int v = 0; v < n; ++v)
{
if(v!=y && vCur[v][x]=='Q')
return false;
}
// check to RT
int xx = x+1;
int yy = y-1;
while(xx<n && yy>=0)
{
if(vCur[yy--][xx++] == 'Q')
return false;
}
// check to LB
xx = x-1;
yy = y+1;
while(xx>=0 && yy<n)
{
if(vCur[yy++][xx--] == 'Q')
return false;
}
// check to RB
xx = x+1;
yy = y+1;
while(xx<n && yy<n)
{
if(vCur[yy++][xx++] == 'Q')
return false;
}
// check to LT
xx = x-1;
yy = y-1;
while(xx>=0 && yy>=0)
{
if(vCur[yy--][xx--] == 'Q')
return false;
}
return true;
}
void solveNQueensBT(int idx, vector<vector<string>>& vRet, vector<string>& vCur, int n)
{
if(idx >= n*n)
{
int cnt = 0;
for(int q = 0; q < n*n; ++q)
{
if(vCur[q/n][q%n]=='Q')
++cnt;
}
// cout << cnt << endl;
if(cnt == n)
vRet.push_back(vCur);
return;
}
// Put 'Q' on the position if possible.
if(CanPlace(idx, vCur, n))
{
int yy = idx / n;
int xx = idx % n;
vCur[yy][xx] = 'Q';
solveNQueensBT(idx+1, vRet, vCur, n);
vCur[yy][xx] = '.';
}
// Skip putting 'Q'.
solveNQueensBT(idx+1, vRet, vCur, n);
}
vector<vector<string>> solveNQueens(int n)
{
vector<vector<string>> vRet;
vector<string> vCur;
for(int y = 0; y < n; ++y)
{
string line = "";
for(int x = 0; x < n; ++x)
line += ".";
vCur.push_back(line);
}
solveNQueensBT(0, vRet, vCur, n);
return vRet;
}
결과
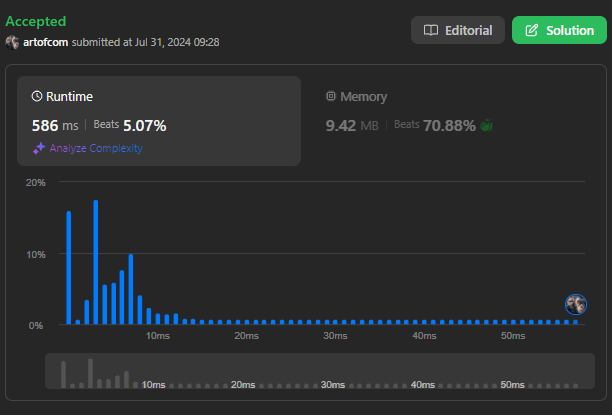
이 방법은 답은 찾아 지지만, 느리다.
더 최적화 해 보자.
N-Queens 조건 상, 하나의 x 축에 두개의 값이 올 수 없다.
그렇다면, x 축에 놓는 값을 하나씩 이동하면서 확인 할 수 있다.
이 x 축으로 놓는 방식을 y 만큼 한다. (문제에서 모두 n)
void NQueens_BT(vector<vector<string>>& vRet, string& strCur, int n, int ix, int iy)
{
if (iy >= n)
{
vector<string> vBuff;
for (int q = 0; q < n; ++q)
{
string strTemp = strCur;
strTemp = strTemp.substr(n * q, n);
vBuff.push_back(strTemp);
}
vRet.push_back(vBuff);
return;
}
for(int x = 0 ; x < n; ++x)
{
int curIdx = iy*n + x;
if (IsValid_NQueens(strCur, n, x, iy))
{
strCur[curIdx] = 'Q';
NQueens_BT(vRet, strCur, n, ix, iy+1);
strCur[curIdx] = '.';
}
}
}
하나의 행에 하나의 Queen을 놓으면 다음 행으로 넘어가면 된다.
결과
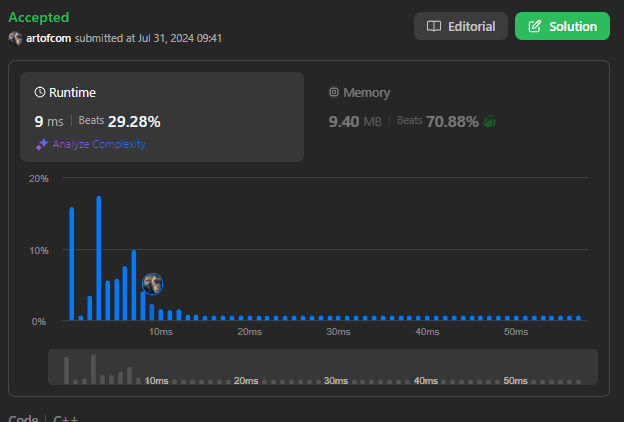
훨씬 근접한 결과를 얻었다.
'Leetcode > NeetCode' 카테고리의 다른 글
| [1D DP][Easy] 746. Min Cost Climbing Stairs (0) | 2024.08.05 |
|---|---|
| [1D DP][Easy] 70. Climbing Stairs (0) | 2024.08.03 |
| [BackTrack][Medium] 17. Letter Combinations of a Phone Number (0) | 2024.07.30 |
| [BackTrack][Medium] 131. Palindrome Partitioning (0) | 2024.07.29 |
| [BackTrack][Medium] 79. Word Search (0) | 2024.07.26 |