https://leetcode.com/problems/trapping-rain-water/description
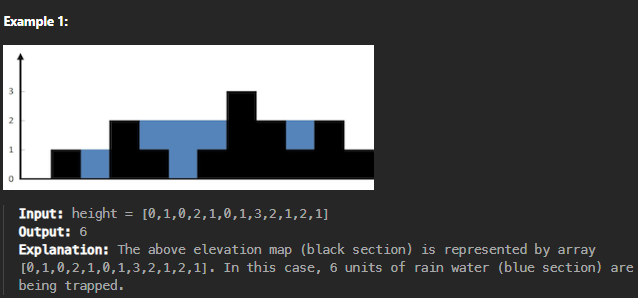
Q. 각 배열값이 기둥의 높이를 의미하는 배열 height 가 주어질 때, 해당 기둥들에 물을 가둔다면, 가둘 수 있는 물의 양을 계산하라.
Solution.
생각해 볼 점이 있는 문제다.
여러가지 방법이 있을 수 있지만, 최적으로 푸는 방법을 찾아 본다.
우선 가둬진 물의 양을 알아내려면 해당 위치 기준으로 이 위치를 가두는 양쪽 기둥의 높이를 알아야 한다.
그리고 이 양쪽 기둥 중, 낮은 기둥과 현재 위치의 높이가 해당 위치의 물의 양이 된다.
예를 들어 2 index 위치에서의 양쪽 기둥은, 1, 3 index 가 되며, 높이는 각각 (1, 2) 이다.
낮은 높이는 1 이므로, 2에서의 높이 0과 1의 차이, 즉 1이 해당 위치에서의 물의 양이 왼다.
5번 index 위치를 보자. 우선 해당 위치의 높이는 0 이다.
가두는 기둥을 찾아 본다.
3(높이 2)과 7(높이 3) 임을 알 수 있다.
따라서 낮은 높이 2와 해당 위치의 높이(0)의 차, 즉 2가 해당 위치의 물 양임을 알 수 있다.
그렇다면, 적절한 양쪽 기둥은 어떻게 구하는가.
이것은 해당 위치를 기준으로 양쪽에서 모이는 방식으로 접근 시, 가장 마지막의 max height 임을 알 수 있다.
로직대로 코드를 만들어 본다.
public int Trap(int[] height)
{
// 오른쪽에서 부터 왼쪽으로 해당위치의 오른쪽 기둥값을 찾는다.
int maxV = 0;
List<int> rightWalls = new List<int>(height);
for(int k = height.Length-1; k >= 0; --k)
{
maxV = Math.Max(maxV, height[k]);
rightWalls[k] = maxV;
}
maxV = 0;
// 왼쪽에서 부터 오른쪽으로 해당위치의 왼쪽 기둥값을 찾는다.
List<int> leftWalls = new List<int>();
for(int k = 0; k < height.Length; ++k)
{
maxV = Math.Max(maxV, height[k]);
leftWalls.Add(maxV);
}
// 현재 위치 높이와 두 기둥중 작은 기둥간의 차가 물 양이 된다.
int ret = 0;
for(int k = 0; k < height.Length; ++k)
{
ret += Math.Min(rightWalls[k], leftWalls[k]) - height[k];
}
return ret;
}
적절한 결과를 얻었다.
Note)
여러 접근이 있을 수 있다.
하지만 이것은 분명 깔끔한 로직접근법 중 하나이고, 이것이 명료해야 코드도 그렇게 된다.
접근법을 기억해 둬야 할 문제중의 하나.
'Leetcode > Challenges' 카테고리의 다른 글
| [Misc][Hard] 41. First Missing Positive (1) | 2024.04.26 |
|---|---|
| [Misc][Medium] 31. Next Permutation (1) | 2024.04.26 |
| [Two Pointers][Medium] 15. 3Sum (0) | 2024.04.24 |
| [Stack][Medium] 155. Min Stack (0) | 2024.04.23 |
| [Sliding Window][Hard] 239. Sliding Window Maximum (1) | 2024.04.19 |