https://leetcode.com/problems/n-queens/description
N-Queens - LeetCode
Can you solve this real interview question? N-Queens - The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other. Given an integer n, return all distinct solutions to the n-queens puzzle. You ma
leetcode.com
Q. n-queens 퍼즐에 맞게 Q 를 n x n 체스보드에 맞게 배치하여라.

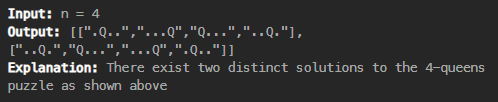
Solution.
역시 backtrack의 일반적인 문제다.
기본 틀에 넣고 문제를 녹여 본다.
체스판에 한번에 두개의 선택이 있다.
Q를 놓느냐 마느냐 이다.
해당 선택을 n x n 번 하였을 때, 놓아진 Q가 퍼즐 규칙에 맞는지 확인 하면 될 것이다.
이런 방법대로 코드를 써 본다.
bool IsValid_NQueens(string& strCur, int n, int idx)
{
// x axis
for (int y = 0; y < n; ++y)
{
bool hasQ = false;
for (int x = 0; x < n; ++x)
{
int index = y * n + x;
if(index > idx) break;
if (strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
// y axis
for (int x = 0; x < n; ++x)
{
bool hasQ = false;
for (int y = 0; y < n; ++y)
{
int index = y * n + x;
if(index > idx) break;
if (strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
// dec
for (int x = 0; x < n; ++x)
{
bool hasQ = false;
int ix = x;
for (int y = 0; y<n && ix<n; ++y, ++ix)
{
int index = y * n + ix;
if (index<=idx && strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
for (int y = 0; y < n; ++y)
{
bool hasQ = false;
int iy = y;
for (int x = 0; x<n && iy<n ; ++x, ++iy)
{
int index = iy * n + x;
if (index<=idx && strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
// inc
for (int x = 0; x < n; ++x)
{
bool hasQ = false;
int ix = x;
for (int y = n-1; y>=0 && ix<n ; --y, ++ix)
{
int index = y * n + ix;
if (index<=idx && strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
for (int y = n-1; y >= 0; --y)
{
bool hasQ = false;
int iy = y;
for (int x = 0; x<n && iy>=0 ; ++x, --iy)
{
int index = iy * n + x;
if (index<=idx && strCur[index] == 'Q')
{
if (hasQ) return false;
hasQ = true;
}
}
}
return true;
}
void NQueens_BT(vector<vector<string>>& vRet, string& strCur, int n, int idx, int cntQ)
{
// n x n 번 수행하면 exit 한다.
if (idx >= n*n)
{
if (cntQ == n)
{
vector<string> vBuff;
for (int q = 0; q < n; ++q)
{
string strTemp = strCur;
strTemp = strTemp.substr(n * q, n);
vBuff.push_back(strTemp);
}
vRet.push_back(vBuff);
}
return;
}
// Q를 안놓거나
strCur[idx] = '.';
NQueens_BT(vRet, strCur, n, idx+1, cntQ);
// Q를 놓거나 해 본다.
strCur[idx] = 'Q';
if (IsValid_NQueens(strCur, n, idx+1))
NQueens_BT(vRet, strCur, n, idx+1, cntQ+1);
strCur[idx] = ' ';
}
vector<vector<string>> solveNQueens(int n)
{
vector<vector<string>> vRet;
string strNow = "";
strNow.resize(n*n);
NQueens_BT(vRet, strNow, n, 0, 0);
return vRet;
}
틀린 방법은 아니지만, 시간이 일반적인 풀이와는 동떨어 지게 나왔다.
최적화를 조금 고려 해 보자.
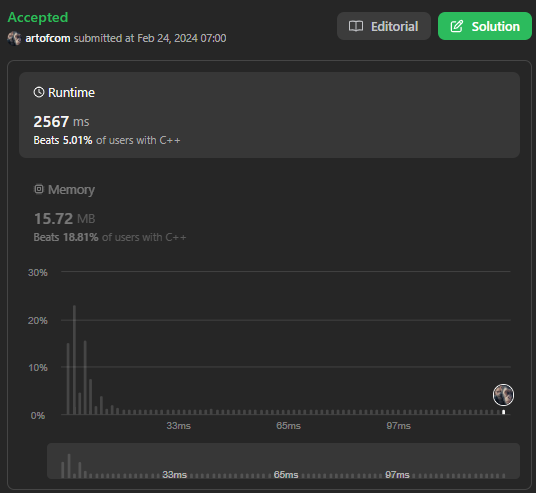
일단 퍼즐 규칙을 재귀 함수 콜을 하기 전에 filter 해 보기로 한다.
또한 n Queen 퍼즐 규칙 중, 첫번째 규칙,
'동일 가로 선상에 Q가 2개 이상 있을 수 없다' 를 조금 먼저 사용해 선택에 적용해 본다.
즉, 하나의 체스블럭이 n x n 개 있는 것이 아니라,
n 짜리 길이에 하나의 Q만을 놓을 수 있는 판이 n 높이 만큼 있다고 생각해 본다.
이제는 높이만큼만 Q를 놓거나 말거나 하면 될 것 같다.
언제? 퍼즐의 규칙에 맞을 때만. (동일 세로줄 X, 대각선에 Q등장 X)
논리를 코드로 작성해 보자.
// 퍼즐 규칙에 유효한지 확인.
bool IsValid_NQueens(string& strCur, int n, int ix, int iy)
{
int x, y;
// check upper direction.
for (y = 0; y < iy; ++y)
{
int index = y * n + ix;
if (strCur[index] == 'Q')
return false;
}
// check up left direction.
for(x = ix-1, y = iy-1; x>=0 && y>=0; --x, --y)
{
int index = y * n + x;
if (strCur[index] == 'Q')
return false;
}
// check up right direction.
for(x = ix+1, y = iy-1; x<n && y>=0; ++x, --y)
{
int index = y * n + x;
if (strCur[index] == 'Q')
return false;
}
return true;
}
// Main BackTrack func.
void NQueens_BT(vector<vector<string>>& vRet, string& strCur, int n, int ix, int iy)
{
// iy가 n번 이상되면 최종연산을 exit한다.
if (iy >= n)
{
vector<string> vBuff;
for (int q = 0; q < n; ++q)
{
string strTemp = strCur;
strTemp = strTemp.substr(n * q, n);
vBuff.push_back(strTemp);
}
vRet.push_back(vBuff);
return;
}
// 한번에 하나씩, n번을 수행해 본다.
for(int x = 0 ; x < n; ++x)
{
int curIdx = iy*n + x;
// 퍼즐 규칙에 맞을때만, 계속 진행 한다.
if (IsValid_NQueens(strCur, n, x, iy))
{
strCur[curIdx] = 'Q';
NQueens_BT(vRet, strCur, n, ix, iy+1);
strCur[curIdx] = '.';
}
}
}
vector<vector<string>> solveNQueens(int n)
{
vector<vector<string>> vRet;
string strNow = "";
strNow.resize(n*n, '.');
NQueens_BT(vRet, strNow, n, 0, 0);
return vRet;
}
수행시간이 많이 개선 되었음을 확인 할 수 있다.
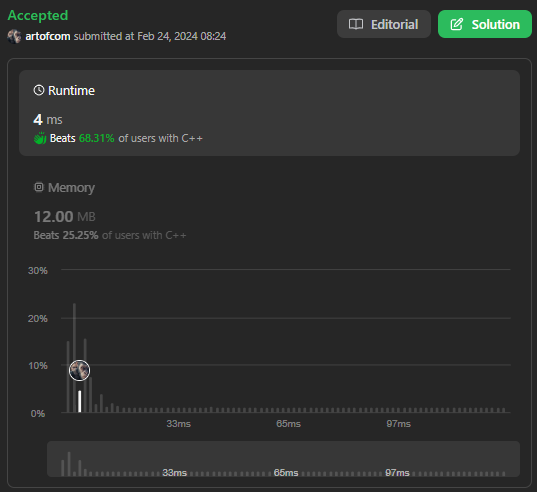
'Leetcode > Top 100 Liked' 카테고리의 다른 글
| [Backtracking][Medium] 79. Word Search (1) | 2024.02.27 |
|---|---|
| [Backtrack][Medium] 78. Subsets (1) | 2024.02.25 |
| [Backtracking][Medium] 46. Permutations (0) | 2024.02.22 |
| [Backtracking][Medium] 39. Combination Sum (0) | 2024.02.20 |
| [Backtracking][Medium] 22. Generate Parentheses (0) | 2024.02.19 |