https://leetcode.com/problems/rotting-oranges/description
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
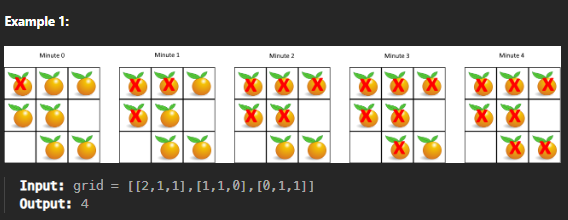
Q. 주어진 grid에서 각 숫자는 다음을 의미한다.

이때 모든 orange가 rotten 상태로 변화는 시간(단계 수)을 구하라.
Solution.
위 문제인 지나갈 수 있는 길에서 모든 길에 도달하는 단계 수를 구하면 같은 문제가 된다.
다만, 이번 문제는 조금 신경써야 할 것들이 있다.
우선 출발 지점이 여러 부분 일 수 있다. 따라서 다중 시작 점을 고려 한다.
또한, 한 지점에서 끝이 아닌, 퍼져 나가는 단계가 중요하므로, 반드시 BFS를 써야만 한다.
이 두 포인트를 유의하면 나머지는 대동소이하다.
논리대로 코드를 써 준다.
// Utility Function. - 특정 index로 진행 할수 있는지 판단한다.
bool orange_canMove(vector<vector<int>>& grid, vector<bool>& vVisit, int idx)
{
if (vVisit[idx]) return false;
int W = grid[0].size();
int iX = idx % W;
int iY = idx / W;
return grid[iY][iX] == 1;
}
int orangesRotting(vector<vector<int>>& grid)
{
int totalCount = 0;
int H = grid.size();
int W = grid[0].size();
queue<int> qBuff; // idx
for (int k = 0; k < grid.size(); ++k)
{
for (int q = 0; q < grid[0].size(); ++q)
{
if (grid[k][q] != 0) ++totalCount;
if (grid[k][q] == 2)
qBuff.push(k * W + q); // 시작점이 여러 부분 일 수 있다.
}
}
// 대상 오렌지가 없다면 진행할 필요 없다.
if(0 == totalCount) return 0;
vector<bool> vVisit;
vVisit.resize(W * H, false);
int time = 0;
int visitCnt = 0;
while (qBuff.size() > 0)
{
int size = qBuff.size();
bool processed = false;
for (int k = 0; k < size; ++k)
{
int curIdx = qBuff.front();
qBuff.pop();
int iX = curIdx % W;
int iY = curIdx / W;
if (vVisit[curIdx]) continue;
vVisit[curIdx] = true;
++visitCnt;
// 실제 진행 과정이 진행되었나 체크 한다.
processed = true;
// up
if (iY>0 && orange_canMove(grid, vVisit, curIdx-W))
qBuff.push(curIdx - W);
// down
if (iY < H - 1 && orange_canMove(grid, vVisit, curIdx+W))
qBuff.push(curIdx + W);
// left
if (iX > 0 && orange_canMove(grid, vVisit, curIdx-1))
qBuff.push(curIdx - 1);
// right
if (iX < W - 1 && orange_canMove(grid, vVisit, curIdx+1))
qBuff.push(curIdx + 1);
}
if(processed) ++time;
}
// 총수가 애초 오렌지 수와 같다면, 모두 visit 했다고 판단 할수 있다.
return (visitCnt==totalCount) ? time-1 : -1;
}
다소 최적화의 여지는 더 있을 수 있으나, 구조는 비슷할 것이다.

Note) 진입점이 여러 부분이라는 점에서 흥미로운 문제.