[Binary Search Tree][Medium] 450. Delete Node in a BST

https://leetcode.com/problems/delete-node-in-a-bst/description

 

Q. 주어진 BST에서 특정 값인 노드를 삭제하라. 

 

Solution. 

 2진트리 삭제 연산 코딩을 확인하는 문제이다. 

 2진 트리의 특성을 유지하면서 특정 노드를 삭제하라면, 

 대상 노드를 삭제하고 어떤 노드를 삭제된 노드의 자리에 위치케 할지를 결정하는지가 알고리즘의 핵심이라 하겠다. 

 

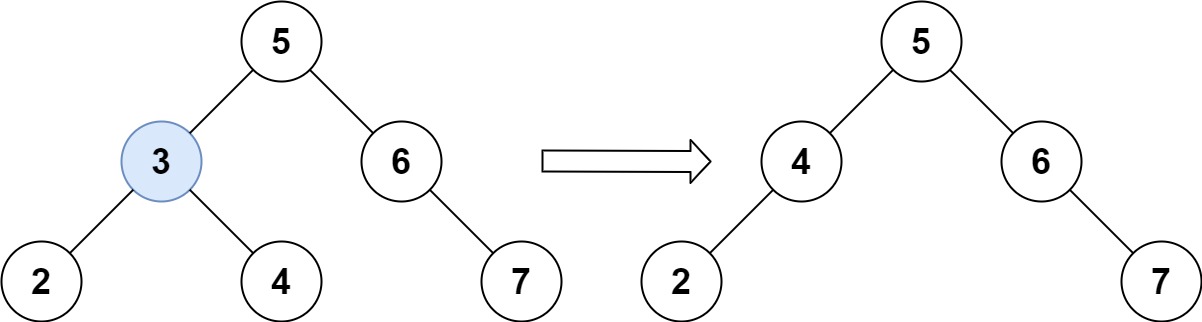
연산 자체는 이런 식이다. 

 

2진 트리에서, 특정 노드를 제거하면,

> 노드의 좌측 사이드에서 제일 큰 값을 가진 노드, 혹은

> 우측 사이드에서 가장 작은 값을 가진 노드 를 해당 삭제된 노드 자리에 위치하면

해당 트리의 특성이 유지된다. 

 

따라서 해당 문제를 풀기 위해서는 

> 특정 노드 탐색

> 특정 노드 기준, child 중 최소 값 노드 찾기 

> 특정 노드 기준, child 중 최대 값 노드 찾기 

> 주어진 정보를 바탕으로 해당 노드를 다른 노드로 교체.

 

위의 연산이 순차적으로 행해져야 한다. 

 

TreeNode* deleteNode(TreeNode* root, int key)
{
    if (root == NULL)	return root;

    TreeNode* target = root;
    TreeNode* parent = NULL;

    // Search Target.
    while (target != NULL)
    {
        if (target->val == key)
            break;

        parent = target;
        if (target->val > key)	target = target->left;
        else target = target->right;
    }

    // Search Smallest Node from the right Child.
    TreeNode* smallest = NULL;
    TreeNode* parent_smallest = NULL;
    if (target!=NULL && target->right!=NULL)
    {
        smallest = target->right;
        parent_smallest = target;
        while (true)
        {
            if (smallest->left == NULL)
                break;
            parent_smallest = smallest;
            smallest = smallest->left;
        }
    }

    // Search Biggest Node from the left Child.
    TreeNode* biggest = NULL;
    TreeNode* parent_biggest = NULL;
    if (target != NULL && target->left != NULL)
    {
        biggest = target->left;
        parent_biggest = target;
        while (true)
        {
            if (biggest->right == NULL)
                break;
            parent_biggest = biggest;
            biggest = biggest->right;
        }
    }

    // Remove target. 
    if (target != NULL)
    {
        TreeNode* replaced = NULL;
        // Replacing with either side is fine.
        if (smallest != NULL)
        {
            if (target->right == smallest)	target->right = smallest->right;
            else parent_smallest->left = smallest->right;
            smallest->left = target->left;
            smallest->right = target->right;
            replaced = smallest;
        }
        else if (biggest != NULL)
        {
            if (target->left == biggest)	target->left = biggest->left;
            else parent_biggest->right = biggest->left;
            biggest->right = target->right;
            biggest->left = target->left;
            replaced = biggest;
        }

        if (parent != NULL)
        {
            if (parent->left == target) parent->left = replaced;
            else parent->right = replaced;
        }
        else
            root = replaced;
    }
    return root;
}

 

 

어쩔 수 없이 코드가 좀 늘어졌지만, 

수행하는 로직은 위의 서술과 대동소이하다. 

 

조금 더 최적화 해 볼 여지는 있는 것 같다.